Converting Turing Machine to an Unrestricted Grammar
Introduction
Converting
to an Unrestricted Grammar
Export
and Parse
Any Turing machine can be converted to an unrestricted grammar.
JFLAP defines an unrestricted grammar as a grammar that is similar to a context-free grammar (CFG), except that the left side of a production may contain any nonempty string of terminals and variables, rather than just a single variable. In an unrestricted grammar, the left side of a production is matched, which may be multiple symbols, and replaced by the corresponding right hand side.
This conversion implements the algorithm in the book “An Introduction to Formal Languages and Automata 4th Edition” by Peter Linz. The algorithm can be founded on page 283-285.
There are 3 major steps that the algorithm follows in order to convert the Turing machine to an unrestrcted grammar. The first step is applying the basic rules from the start variable. It allows the grammar to generate an encoded version of any string q0w with an arbitrary number of leading and trailing blanks. The second step is applying generating the production for each transition of Turing machine. The last step is applying additional rules to our productions if we enter one of final states of TM, so we can derive terminals.
We will now convert the TM into an unrestricted grammar. First, open up the Turing Machine window and load the file verysimple_TM.jff.
Click on the Convert → Convert to Unrestricted Grammar menu option, and the following screen should appear :

This is a very simple Turing machine that accepts any language that has one or more “a”s. Just like other conversion windows, you can click the What's Left? button to view what states or transitions remain to be converted.
Now, let's produce our first
productions for our new grammar (the first step of algorithm). By
default, there are going to be 3 productions that are going to be
produced for every TM that is going to be converted. These three
rules are
“S->V(==)S, S->SV(==), S->T”, where S is
the start variable. In addition there are going to be 2 additional
rules “T->TV(aa), T->V(a0a)”, in which “a” refers to
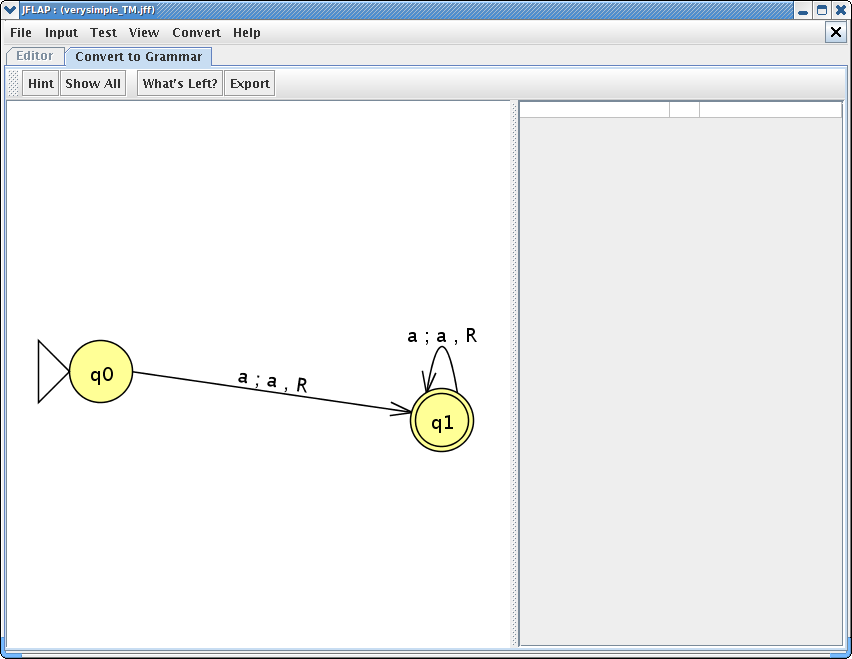
for all readable strings in the tape. The result of productions
generated by the first step can be viewed by clicking initial state
q0. Note that “=” refers to the blank tape symbol in the Turing
machine. After clicking the state q0, your window would look like
this :
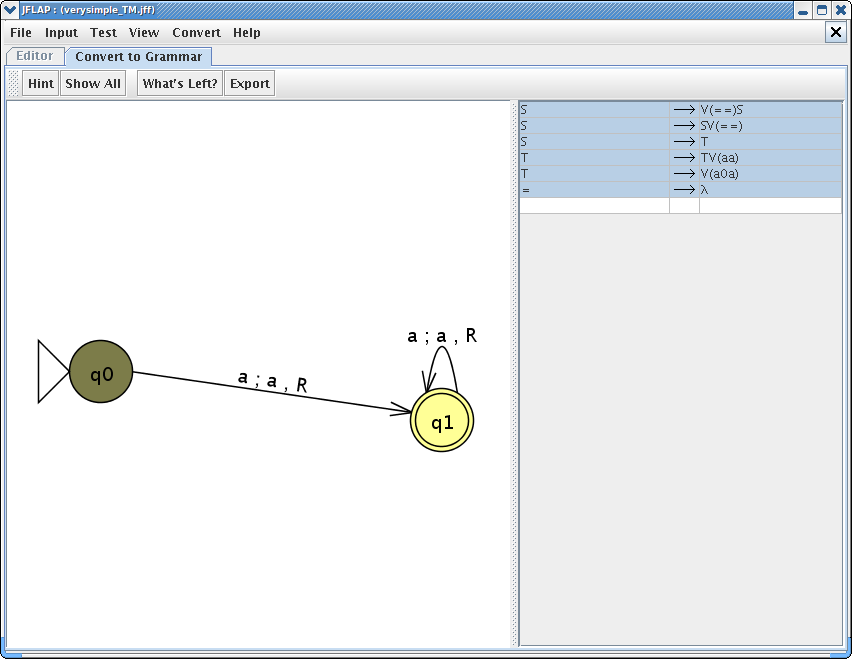
Now, let's move on to the second step of algorithm and examine our first transition from q0 to q1. The transition is (q0, a) => (q1, a, R). By following the algorithm, we are going to place production V(x0a)V(yz) → V(xa)V(y1z), where x, y is all elements of input alphabet+blank symbol and z is all elements of the tape alphabet. Since we only have “a” in our input alphabet our x and y is going to be “a”. “z” can be either “a” or “=” (blank). Also, since q1 is final state, we have to apply the last step of algorithm . We apply the special rule V(a1a) → a and yV(xz) → a, where x and y are all the input alphabet + blank symbol (=) and z is all of our tape alphabets. By doing so, we can generate terminals on the right hand side of productions. After applying all of these rules, our grammar window would look like :
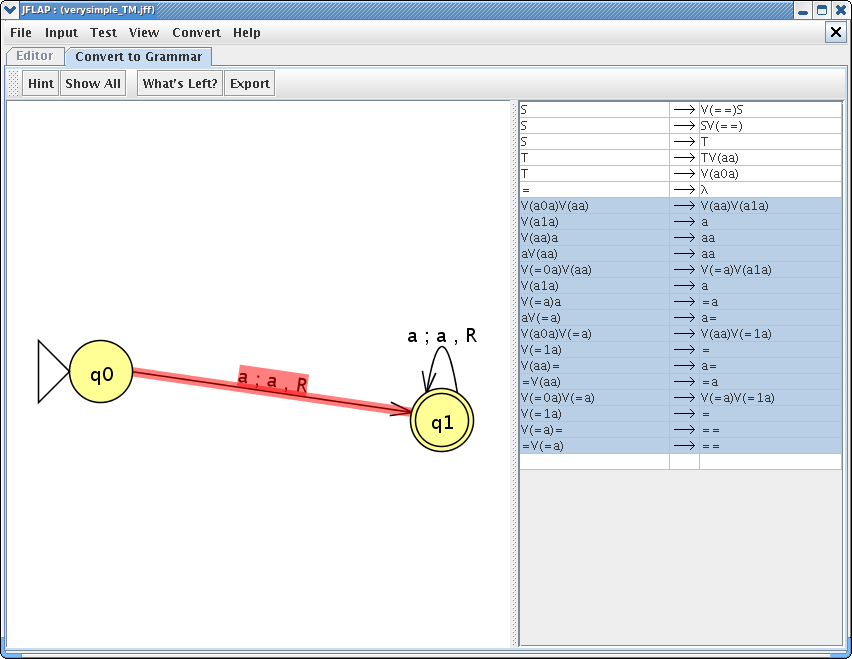
After either clicking our last transition in q1 or using Show All button, we can finish our conversion.
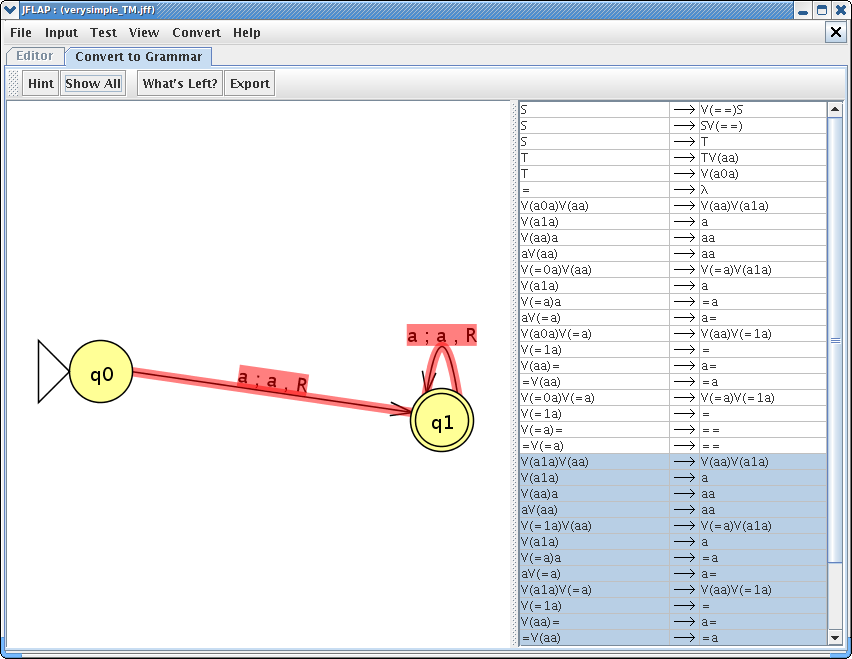
Let's now export this converted grammar. You can click on Export button to export this grammar. After exporting the grammar, your window would look like this :
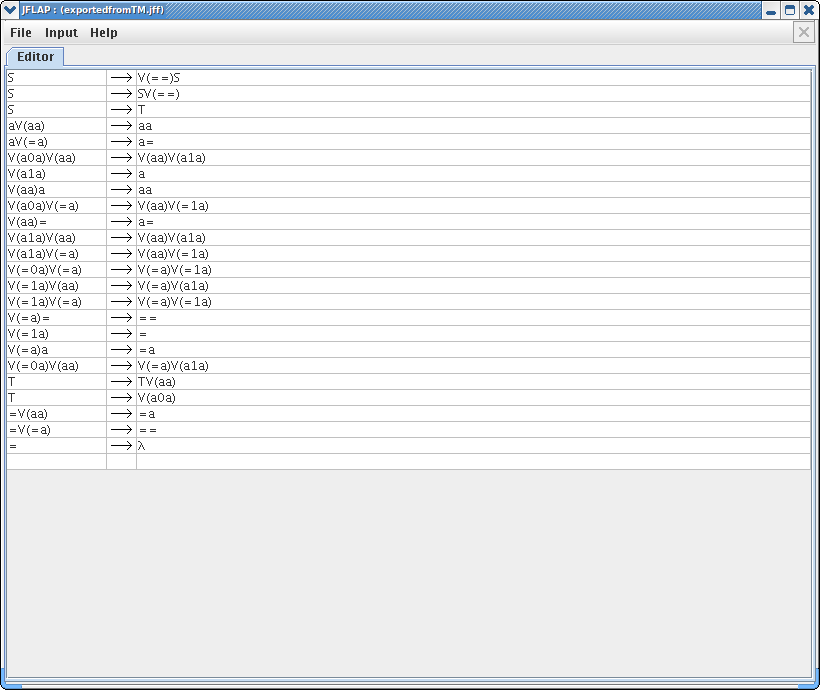
Now let's try to parse this unrestricted grammar, note that V(aa) is actually refers to one variable. Click on Input and Parser for Converted Grammar from TM. You will see very similar grammar parse pane from brute force parsing. In this parser, all the variables such as V(aa) is trimmed into regular variable like “A” or “B”, so the parsing can occur. This trimming procedure is done internally in the parser. In the input, type in string “aa”. You can see that the this string is accepted by the language as expected. Click on STEP buttons several times to see how we derive this string. You can either view the derivation in Noninverted tree or Derivation table. Your result should look like one of these windows.
NOTE: The JFLAP Parser recognizes this special notation in the grammar. It converts varaibles such as V(aa) into normal variables like “A” in the background to facilitate the parsing.
WARNING: This only works with very small examples since the conversion is exponential.
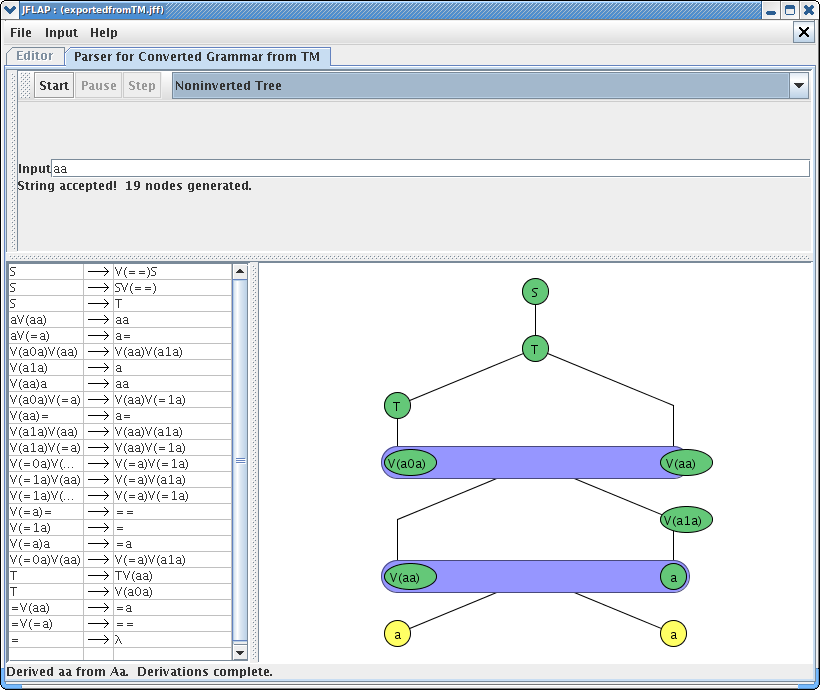
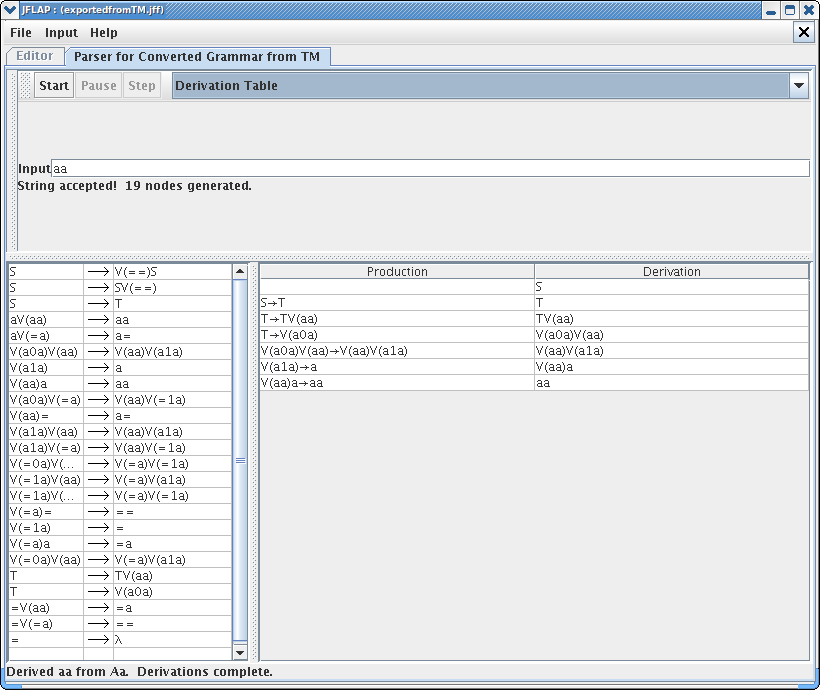
Now let's try to input “aaaaaaaa” (8 a's). The parser quickly accepts the language, but note that there are 271 nodes generated for such a simple string. This reveals that the parser is going to have really hard time parsing other complicated grammar such as a^nb^nc^n. As Turing machine gets more complicated, the parsing of converted grammar would get more difficult and almost impossible. Although the converted grammar might not be useful in actually checking the string, it proves that TM can be converted to unrestricted grammar.
NOTE: You can also use user control parser to derive the string manually.
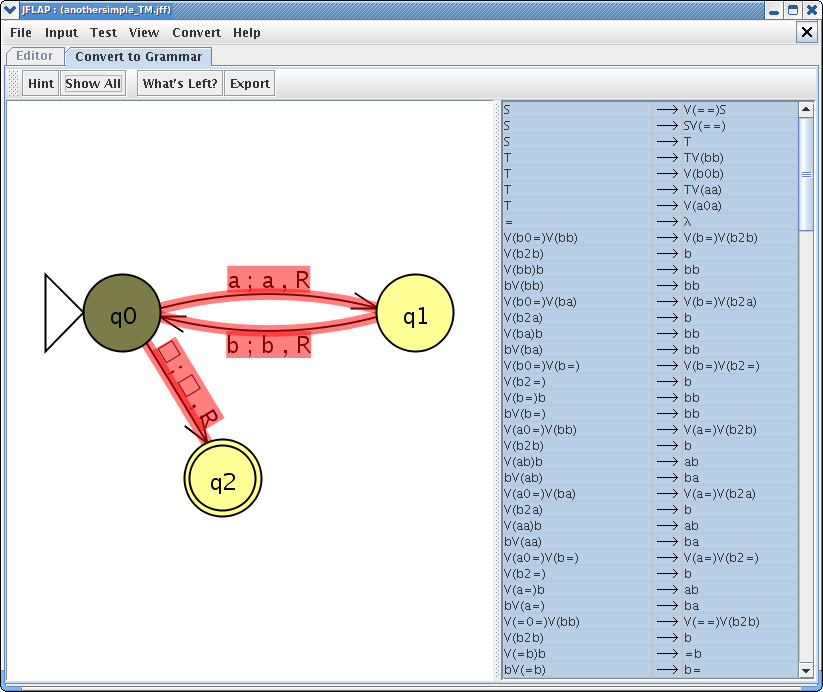
Another example of converting TM to unrestricted grammar is shown in below windows. You can load the file anothersimple_TM.jff to load this example. Note that it generated 21578 nodes to just to accept simple string “ab”.
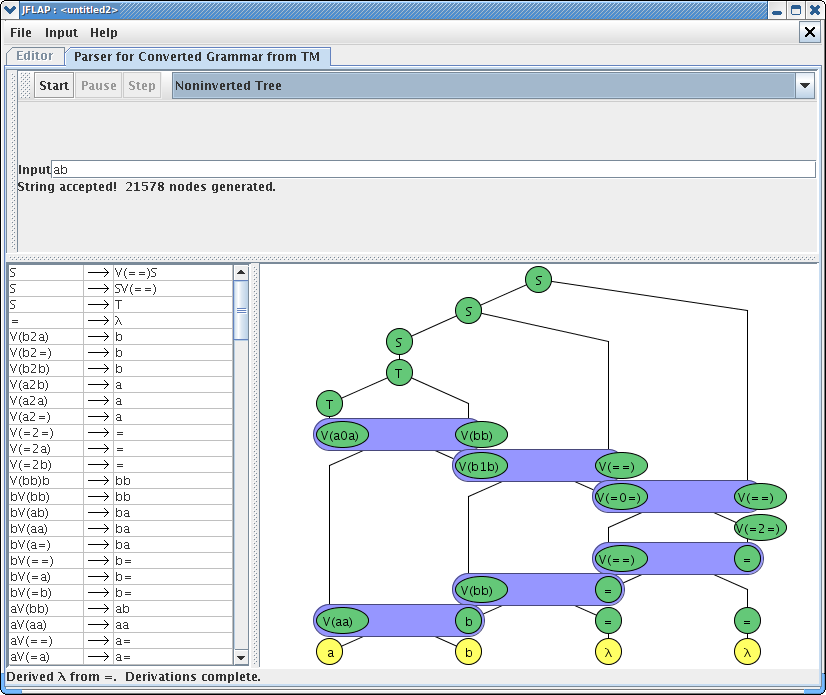
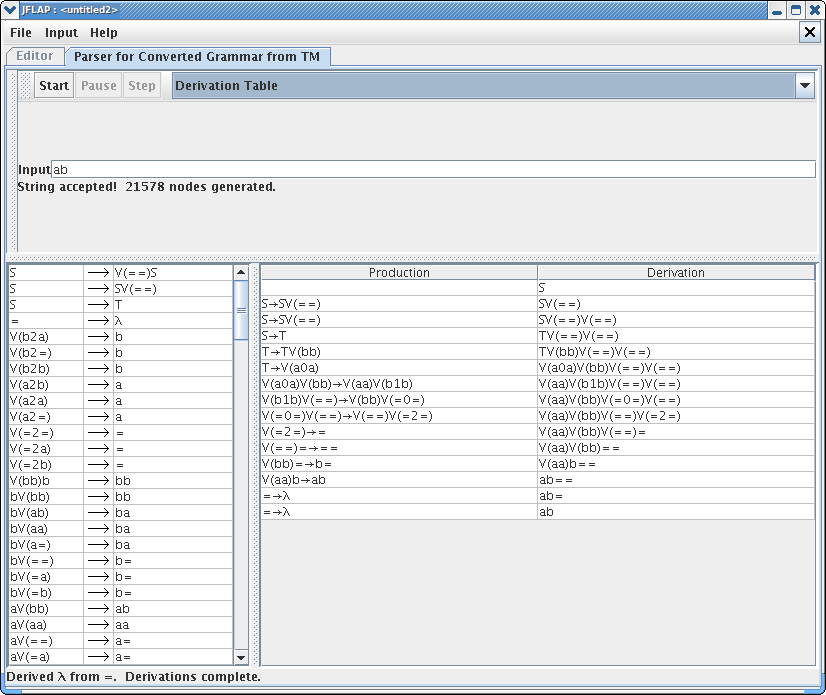
This concludes our brief tutorial on converting Turing machine into an unrestricted grammar. Thanks for reading!